Contents

1. Combinatory Declarative Programming

2. Competition "Programmer 02"

Introduction

For over a decade several groups of researchers, working independently, have developed a variable-free, combinatory relational approach to declarative programming and applied it to different components of the programming cycle (development, refinement, transformation, static analysis, compilation) or used it as a declarative extension in its own right.

Each member group has had its own unique perspective on the use and development of these techniques, although there is at present a substantive core where all these approaches overlap, suggesting that a new area within declarative programming has come into being in this work.

The techniques draw on ideas from an unusually wide range of areas: relation calculus, database query evaluation, rewriting, combinatory logic, program synthesis and transformation, denotational semantics, program algebra, computational set theory, set constraints, and graph and category theory.

We briefly summarize some of the components of the work below, and the contributions of the research groups.

The Relation Calculus

In the 1940's Tarski introduced a first-order axiomatization of calculus of binary relations with operations (union, intersection, composition, converse, complementation) and constants ,0,1 (identity, diversity-its complement, and the empty and universal relation, consisting of all pairs) leading to the subsequent definition of relation algebras. Tarski and his collaborators found that the relation algebra equipped with the relational counterpart of constructors and destructors of pairs, and certain variants could provide a variable-free foundation for most of mathematics. Much of this work is set forth in [60], where the authors speculated that some of their results might be useful in computer science. It has certainly proved to be the case.

Variable-free approaches (of an entirely different character) to logic and computation have a long history: they were first discovered by Shönfinkel in the 1920's, and developed extensively by Curry and Feys in the 1940's and 50's, among others. Their work was later exploited by researchers in semantics and in the compilation of functional programming [61]. A combinatory approach to program development and analysis was developed by Backus [27] in his point-free Algebra of Programs. A combinatory-logic based approach to higher-order unification was described in [6].

Relations

The calculus of relations has been used extensively in computer science, of course, and logic programming itself can be described as a relations-based paradigm. But our focus here is on their combinatory development. Combinatory, or point-free relation calculi have been applied to the specification and synthesis of functional programs, data types, and the derivation of general programming principles, by Roland Backhouse and his collaborators at Eindhoven[25,26], and further by Bird and De Moor [32], using Freyd's allegories [46], a categorical relational formalism.

Allegories have also been used in relational approaches to hardware design [33,48,37].

The database community has worked with query processing and optimization using relation algebra since Codd's pioneering work in the 1970s, probably the greatest single application of the formalism in computer science. Although this work is not directly related to the subject at hand, some of the researchers in combinatory logic programming came from the relational database community.

Other Variable-free Formalisms

No attempt is being made at an exhaustive description of the combinatory approach, elusive a concept as it is. Quine's predicate-functor logic, used by Hamfelt, Fischer Nilsson and others (see below) for Combilog is another example, as are the many codifications of logic in other theories, e.g. graphs, throughout the literature of mathematical logic.

Category Theory itself may be described, at least in part, as an effort to eliminate variables from mathematics. It has also been exploited to give a new foundation for logic programming by Martini, Corradini, Asperti, Montanari, Power, Kinoshita, Diaconescu, Finkelstein, Freyd, Amato, McGrail, Lipton and Pym, to name a few of the researchers in the field. This approach to logic programming is quite different in character, and deserves a treatment of its own. It will not be further discussed here. See e.g. [3,4,47,1,42,41,2].

Combinatory Logic Programming

It is, perhaps, surprising that these techniques were not applied (to this author's knowledge) until relatively recently (early 1990's) to logic programming. Since then however, three or four research groups have begun to systematically develop combinatory approaches to logic programming in a number of ways. Combinatory relation calculi similar to Tarski's calculus of relations and Quine's predicate functor logic are used as a variable-free target language by three groups of researchers, whose work is further described below:

• Formisano (Perugia), Omodeo (L'Aquila), Policriti (Udine) and Simeoni (Venice).
• Hamfelt (Uppsala), Fischer Nilsson (DTU-Denmark), Vitoria (Lisbon)
• Lipton (Wesleyan), Broome (Maryland), Chapman (New York)

The idea of taking a combinatory approach to logic programming originated (to the author's knowledge) with Jørgen Fischer Nilsson's 1990 paper [8] where the term ``Combinatory Logic Programming'' first appeared in print. A categorical variable-free formulation of a very different nature, due to Martini and Asperti, appeared the year before [23], but it is not a combinatory approach (see comments on categorical formulations, above). Broome and Lipton [35,43,44] began working in the area in the early 1990s.

An example

It may be most instructive to see a small example of a combinatory translation of a logic program. This example is deceptively simple, but gives some idea of the fundamental notions involved.

Consider the following Horn Clause program defining the transitive closure of a graph
 

and the queries

      | ?- conn(a,c).             
      | ?- conn(X,c).

This rather carefully chosen example can be easily reformulated in first-order-variable-free relational terms denoting binary relations on the Herbrand universe , as follows. We introduce the binary relation variables and and translate the program into a pair of relation equations. We denote composition of relations by `` '' .

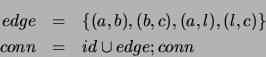
where denotes the identity relation. Thus the second line states, in a point-free way, that .

The queries are then represented by the relation expressions:

where is the universal relation , (hence represents the set of all pairs whose second component is ).

Some questions that arise naturally at this point are: can such a translation be defined for an arbitrary Horn Clause program, or even for extensions of conventional programs, what kind of relation calculus is suitable for it, and can the resulting relational expressions be easily executed, controlled and optimized?

The research groups whose work is discussed below apply different techniques to obtain point-free versions of arbitrary logic programs and provide different notions of target language execution, sometimes with different aims. Fischer Nilsson and Hamfelt define a programming language, Combilog, based on a small set of predicate-forming operators and a set of inference rules, and a meta-interpreter to execute expressions in the language. They are able to achieve very compact representations of programs by means of recursion operators such as foldr. As an example, the program for append

in the fold-extended COMBILOG becomes

where swaps the two first arguments (since foldr differs from append in that the second argument, not the first one, is the recursion parameter).

Broome, Chapman and Lipton define a (binary) relational programming language, Ralog, a relational abstract machine based on rewriting, and a relational constraint processing engine based on constructive negation. Formisano, Omodeo, Policriti and Simeoni also use the Tarski-Givant formalism as a basis for their work, but exploit it in different ways: for automated deduction with different graph and set theories, and for formal comparison and analysis of these ontologies. All three groups make use of a variable-elimination algorithm to translate predicate logic into a point-free combinatory formalism.

Our summary here is not exhaustive, there have been other groups involved in similar projects: Bellia and Occhiuto develop a declarative algebra of programs (C-expressions) that captures unification, rewriting and narrowing in [29]. A compositional relational approach to logic programming is also described in [52]

The descriptions below have been contributed by members of the research groups involved, and edited for this report by the author.

Hamfelt and Fischer Nilsson: Compositional Predicate Operators

It is well-known that functional programs can be coined into variable free program expressions by appealing to a system of higher-order functions taking ordinary program functions as constants. Our concern is relational programming using logical clauses rather than functional programming.

We introduce a variable-free compositional form of definite clausal logic programs based on a system of predicate-forming operators proposed by Quine. The semantics is given by a simple fixpoint construction accomplished solely by iterated union, intersection, a generalised projection, and list construction and deconstruction. In addition a system of proof rules devises a proof theoretical semantics which is proved equivalent to the suggested fixpoint semantics. Moreover the predicate operators are proved sufficient with respect to expressivity for definite clauses over list terms and a logic programming metainterpreter is set up. With recursion operators being added we have results on applications to compositional programming and inductive logic programming reported in [12].

We define a novel view of logic programming in which the resolution mechanism for definite clauses is supplemented with goal and problem reduction oriented proof structure reflecting the high level structure of a program shaped by certain operators. The operators used for composing programs come with perspicuous inference rules which lay open the goal-directed computation behavior. The program operators constitute a tool for composing programs at a structural level above clauses.

The dispensing with variables facilitates manipulation of programs and transformations by means of algebraic rewriting rules, since the only remaining variables are variables ranging over subprograms, that is predicate terms. The compositionality of the predicate term semantics ensure that programs represented by predicate subterms function fully independently of the embracing context, further easing use of algebraic rewriting. This is in contrast to usual clausal formulations, where variables in terms links to the embracing constructions. This is analogous to the the -calculus vis à vis combinatory logic.

In particular, the variable-free form of operator programs facilitates manipulation of programs in a metalogic programming setting. This is exploited in an innovative method for induction of logic programs in [12].

Formisano, Omodeo, Policriti & Simeoni: A description of our research activity on the calculus of relations

The Tarski-Chin-Givant formalism is a modernized version of the Pierce-Schröder formalism of dyadic relations. It offers an assembly language for equational logic of a lower level than first-order logic. Its constructs operate on relations, very much like the constructs of Codd's relational algebra operate on relations of any degree; in , however, relations can have an infinite cardinality, and complementation w.r.t. the full domain of discourse is available as an operation.

The possibilities of use of the calculus of relations in automated deduction are described in [20] and in [21], where the authors outline different research themes and pave the way for the subsequent work. In particular, in [21] we have abstractly specified important data types such as nested lists and sets ultimately based on individuals, on top of which one can easily define further types (e.g., a line editor).

In [16] we touch different themes related to relational reasoning, among others:

• The emulation of through first-order logic (e.g., within Otter, or within a more markedly equational theorem prover). Far from being a vicious circle, this has led to a finite axiomatization of ZF set theory.

• Initial steps in the development of a platform specifically oriented to relational reasoning.

Automated techniques to translate first-order formulas into the relational formalism are dealt with in [17]. Algorithmic techniques are presented (by means of several examples taken from different application scenarios) together with an analysis of their computational complexity. The exposition is made clear by exploiting a graphical representation for expression over relations.

The possibility of exploiting a general-purpose theorem prover in order to mechanize relational reasoning has been investigated in [18,19,22]. In these works we design and develop a structured proof-methodology aimed at using a first-order theorem prover (in the case, Otter from the Argonne National Lab.) as a kernel engine for reasoning with relations. In particular, in [18,19], we show how the adoption of a rigorous and structured approach in developing the experiments immediately allows one to build a hierarchy of axiomatizations. At each layer of this hierarchy one introduces new relation constructs and proves their properties. This approach permits a better guidance of the behavior of the underlying theorem-prover, since during the proof-search, the focus tends to be posed on the laws/constructs strictly related to the theorem being proved. Higher is the layer in the hierarchy of axiomatizations, higher is the semantical complexity of the laws to be proved and of the involved constructs.

As an interesting side-effect, this approach guarantees great independence from the specific theorem-prover used as kernel inference-engine.

Broome, Lipton & Chapman: Declarative Relational Programming

Our research explores how Logic Programming itself may be profitably understood, extended and compiled in terms of an underlying equational relational calculus, in which relation variables play a fundamental role, similar in some regards to the role of function variables in the lambda-calculus. The variables in the resulting terms correspond to predicate (second order) variables in the original program, whereas all first order variables are eliminated.

In this work we use an equational extension of the relation algebra formalism (with a fixed-point operator and relations corresponding to permutations, projections and constructors of terms) as an executable algebra of logic programs. We translate logic programs into combinatory relation expressions, which are then executed via rewriting and output-formatting algorithms.

Since at any moment during execution, the partially-evaluated program is a bona-fide ``declarative'' mathematical object (a relation expression), the language makes available to the programmer direct manipulation of the fringe of the SLD tree. This provides a new approach to control, optimization, and manipulation of state. The relation calculus admits a more general notion of query and output (compound relation and set-expressions), as well as propagation of relational constraints during execution and extensions to higher-order logic.

Our Research in this area makes use of other relational formalisms (Freyd's allegories) which incorporate type and constraint information into the compilation language, and a more general notion of program, queries and outputs (first-order queries, extensions to equational logic and constructive negation as well as higher order logic).

Computation in this formulation means relation calculus rewriting of queries (relation expressions) to members of some distinguished class of relation expressions (usually recursion-free terms), followed by representation of such expressions in a human readable form in a way that depends on the data domain, a process here called printing.

query solution

In the Ralog programming language, data means terms in a Herbrand Universe, and printing is application of the quantifier elimination algorithm in constructive negation.

Future Directions

The research in Combinatory Declarative Programming raises many interesting questions. What special techniques will be needed for efficient compilation of these new combinatory expressions? What point-free calculi are most suitable for different declarative extensions? There is a great deal of formal similarity between the techniques outlined here and calculi used for program synthesis. It would seem that this opens up new possibilities for transfer of techniques and semantics between the two areas.

The submission deadline was 23 November 2002. Information about this competition was distributed to different schools, Lyceums, Universities of Moldova. Twenty-one submissions received from eleven different institutions, by 23 November 2002 which were divided in three different levels:  Specialists, University and college students, Lyceum pupils.

On 1 December 2002  only thirteen participants were able to participate in two levels: Lyceum pupils and Specialist. Computers were randomly distributed between all the participants half an hour before competition (for preparing for competition), and then disconnected from LAN. 

The competition last for three hours, and provided three problems: Pawns, Rebus and The Farmer.  The problems were selected by the competition committee from a multitude of other problems 15 minutes before competition starts (by voting of committee members). The competition committee consisted of three members, specialists from three different Universities:

1. Vitalie Cotelea, Ph.D., Academy of Economic Sciences
2. Victoria Boghanastiuc, Ph.D., Politechnical University of Moldova
3. Serghei Pelin, master of science, The University of Applied Sciences of Moldova

Immediately after the time was up, the competition committee thanked every participant and wrote down the results. The winners are:

• Lyceum level: Alexander Pelin (picture on the left)
  • lyceum pupil, XII-grade, real profile, specialization - "Informatics and mathematics", Lyceum nr. 2 - "Gaudeamus", Chisinau, Moldova)
• Specialists level: Ian Orlovski (picture on the right)
  • master of science, logic programming lecturer at the University of Applied Sciences of Moldova

The announcement and awarding of the winners took place on 5 December 2002 before the scientifico-metodical conference for the 10th anniversary of The University of Applied Sciences of Moldova.

Every participant was awarded by a certificate of participation, a set of three books on Logic Programming published in the University of Applied Sciences of Moldova and a CD with different information and programming languages.

The competition winners were awarded with Visual Prolog Professional (on behalf of Prolog Development Center, Copenhagen), financial contribution from COLOGNET - 100 EURO, and a financial contribution from University of Applied Sciences of Moldova - 500 Lei.

The results of this competition shows, as it was expected, that using of logic programming languages permits to obtain higher results, in shorter terms. This can be a good example for further popularization of Logic Programming in Moldova.

We hope to organize this competition in the future.